Công thức tính đạo hàm cung cấp cho học sinh các công thức liên quan đến đạo hàm. Các công thức này giúp các bạn học sinh có thể tham khảo, đồng thời vận dụng được trong quá trình học Toán. Cùng trungtamHoaHocTro tìm hiểu các công thức này nhé!
Khái niệm đạo hàm
Theo Toán học, đạo hàm là tỉ số giữa số gia của hàm số và số gia của đối số tại một điểm được gọi là XO. Kho số gia tiến dần tới số 0 thì đó được gọi là đạo hàm của hàm y = f (x) tại XO.
Đạo hàm của hàm số y = f (x) ký hiệu bằng y’ (XO) hoặc f ‘(XO)
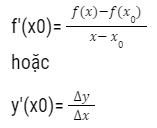
- Số gia đối số: Δx = X – XO
- Số gia hàm số: Δy = Y – YO
>>>>> Xem thêm: Trung tâm gia sư uy tín ở Đà Nẵng
Các quy tắc cơ bản
| (C)’ = 0
Đạo hàm với hằng số bằng 0 |
(U ± V)’ = (U)’ ± (V)’
(U1 ± U2 ± … ± Un)’ = (U1)’ ± (U2)’ ± (U3)’ … (Un)’ Đạo hàm 1 tổng bằng tổng các đạo hàm |
| (U.V)’ = (U)’V + (V)’U | 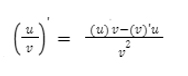 |
Quy tắc đạo hàm cho hàm hợp
Nếu y = y [U (x)] thì y’ (x) = y’ (u) . u’ (x)
Tổng hợp công thức đạo hàm
1. Công thức đạo hàm
- (U + V)’ = U’ + V’
- y’x = y’x.ux
- (U.V)’ = U’V + UV’
- (K.U’) = K.U’
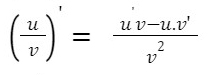
>>>>> Xem thêm: Phòng dạy học cho thuê ở Đà Nẵng
2. Công thức đạo hàm sơ cấp

>>>>> Xem thêm: Bật Mí 3 Phương Pháp Học Toán 12 Hiệu Quả Nhất
3. Công thức đạo hàm cao cấp
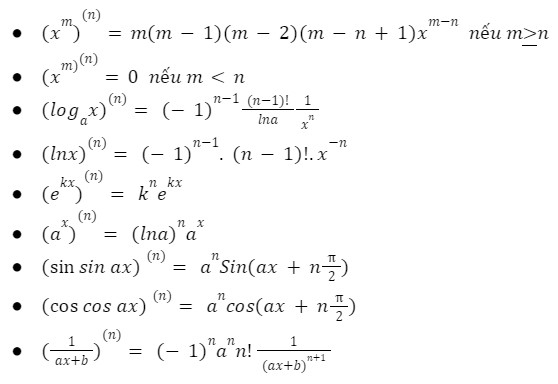
>>>>>> Xem thêm: Mẹo Cách Học Toán Cho Người Mất Gốc Hiệu Quả
4. Công thức đạo hàm lượng giác
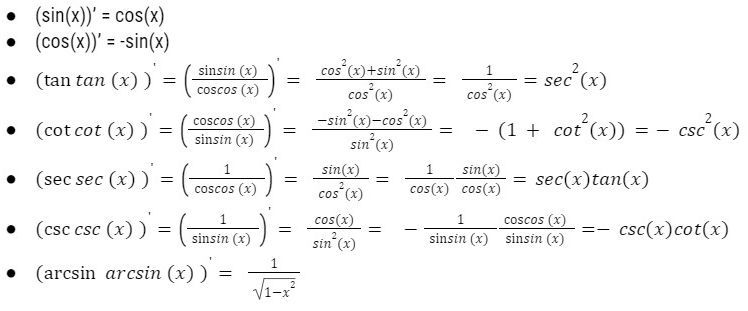
>>>>> Xem thêm: Kinh nghiệm tìm gia sư Toán cấp 2 giỏi, uy tín tại Đà Nẵng
Bảng công thức tính đạo hàm

Một số dạng toán liên quan đến công thức đạo hàm
Dạng 1: Dùng khái niệm tính đạo hàm
Đây là một trong những dạng toán cơ bản trong giải tích. Các bạn chỉ cần dựa vào công thức cơ bản là có thể áp dụng tính được một bài chính xác.
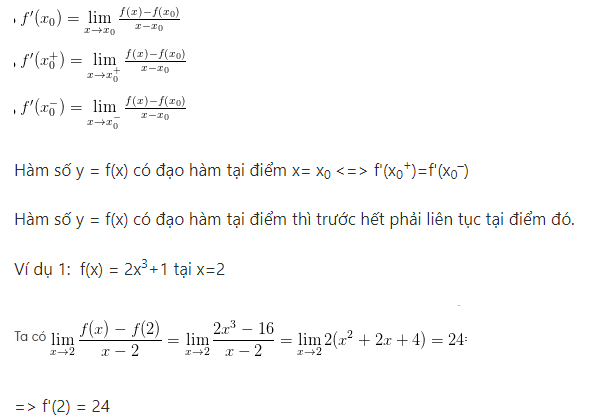
Dạng 2: Chứng minh hằng đẳng thức liên quan đến đạo hàm
Dạng toán này chú trọng vào việc chứng minh dựa trên điều kiện có sẵn. Đòi hỏi bạn phải chứng minh và tính toán thật chính xác để có được kết quả đúng.
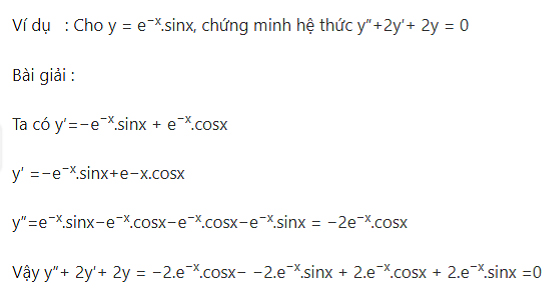
Dạng 3: Tiếp điểm, viết phương trình tiếp tuyến
Đây là một dạng toán phổ biến. Cụ thể là có một phương trình tiếp tuyến của hàm số trên đồ thị đường cong (D): y = f(x) tại tiếp điểm N (x0 ; y0) và có dạng y = y’ (x0) (x-x0) + y0.
Ví dụ minh hoạ:
Cho hàm số y= x3 + 3nx2 + ( m+1)x + 1 (1), n là một tham. Tìm các giá trị của n để tiếp tuyến của đồ thị của hàm số tại điểm có hoành độ x = -1 và đi qua điểm B (1;2).
Tập xác định: D = R
y’ = f'(x)= 3×2 + 6nx + n + 1
Với x0 = -1 => y0= 2n -1, f'( -1) = -5n + 4
Phương trình tiếp tuyến tại N (-1; 2n – 1) : y= ( -5n + 4 ) ( x+1) + 2n -1 (d)
Ta có B ( 1;2) ∈ (d) <=> (-5n + 4).2 + 2n – 1 = 2 => n = 5/8
Dạng 4: Cho hệ số góc viết phương trình tiếp tuyến
Viết phương trình tiếp tuyến Δ của ( D ) : y = f( x ), biết Δ có hệ số góc là H cho trước
Gọi I (x0 ; y0) là tiếp điểm. Tính y’ => y'(x0)
Phương trình tiếp tuyến Δ có hệ số góc H => y’ = ( x0 ) = H (i)
- x0 => y0 = f(x0) => Δ : y = H (x – x0 )+ y0
Chú ý: Hệ số góc H = y'( x0 ) của tiếp tuyến Δ thường cho kiểu gián tiếp.
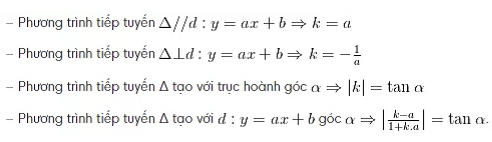
Ví dụ minh hoạ:
Cho hàm số y= x3 +3 × 2 – 9x + 5 (D). Tìm tiếp tuyến có hệ số góc nhỏ nhất trong tất cả các tiếp tuyến của đồ thị (D).
Ta có y’ = f'(x) = 3 × 2 + 6x – 9
Gọi x0 là hoành độ tiếp điểm của tiếp tuyến, vậy f'( x0) = 3 x 2 + 6 x 0 – 9
Ta có 3 x02 + 6 × 0 – 9 = 3 ( x02 + 2 × 0 + 1) – 12 = 3 (x0+1) 2– 12 > – 12
Vậy min f( x0) = – 12 tại điểm x0= -1 ; y0 = 16
=> Phương trình tiếp tuyến cần tìm: y= -12x + 4 <=> y= -12( x+1)+16
Dạng 5: Giải phương trình và bất phương trình bằng đạo hàm
Dạng này sẽ kết hợp nhiều công thức để giải một phương trình hoặc bất phương trình. Được kết hợp để tính toán đưa ra kết quả cuối cùng.

Dạng 6: Áp dụng công thức tính đạo hàm giải bài
Dạng này đòi hỏi các bạn phải thuộc công thức tính đạo hàm cơ bản. Để có thể giải được bài một cách chính xác nhất. Nếu các hàm số phức tạp, có thể áp dụng các rút gọn hàm số. Sau đó, tiến hành đạo hàm.

Dạng 7: Phương trình tiếp tuyến tại điểm cho trước thuộc đồ thị có hệ số góc cho trước
Bạn phải nắm vững được hai dạng viết phương trình tiếp tuyến cơ bản sau.


Dạng 8: Tính đạo hàm cao cấp
Đạo hàm cao cấp là các dạng bài về tính đạo hàm cấp hai trở lên. Khi giải bạn có thể áp dụng công thức: y(n) = (y(n-1))’
Trường hợp tính đạo hàm cấp n. Bạn phải đảo hàm từ cấp 1, 2, 3… Sau đó mới tìm được công thức tính đạo hàm cấp n. Thường dạng này sẽ áp dụng phương pháp quy nạp toán học để chứng minh công thức.
Bài viết trên là tất cả công thức tính đạo hàm. Các bạn học sinh có thể tham khảo để nắm chắc kiến thức và đạt được kết quả môn học như ý.
>>> Tham khảo thêm tại đây:


